konstruktive Interfernz an einer Seifenblase

Interference and Diffraction

Waves are diffracted if they hit an obstacle. So even for light this phenomen can be seen but not always. Due to diffraction, interference is visible under certain circumstances which will be investigated in this article.

1 Diffraction and interference with a candle
experiment setup

Light the candle, Darken the room and make a narrow gap with two pencils.

Describe your observation.

Why does light widen and why does colors appear and why in this order?

With this simple experiment we can show the limits of geometrical optics. Just simple but but not easy at all.

enactive

2 diffraction of light
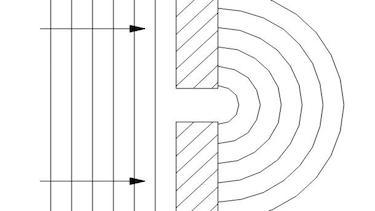
diffraction of a wave

Laser light passes through a single slit. If the width of the slits is smaller than the wavelength of the laser light, the light is diffracted into cylindrical waves. This phenomenon is called diffraction.

The spreading of the waves into the area of the geometrical shadow can be modeled by considering small elements of the wavefront in the slit and treating them like point sources.

In the center these point waves do travel in phase and interfere constructive, this means you see a bright spot on a screen. At the edge the waves do not travel in phase and interfere destructive. By a phase shift of 180 degree the light is wiped out. This phenomenon of bright and dark spots is called interference.

3 displacement of diffraction pattern
diffraction pattern

If you have a more detailed perspective you will see an diffraction pattern. Given Distance $D$ between the slit and a screen and the slit width $a$, the displacement $x$ between to maxima on a screen, can be calculated with:

$$x=k\cdot \frac{\lambda D}{a} \: \text{with}\: k \in \mathbb{N}$$
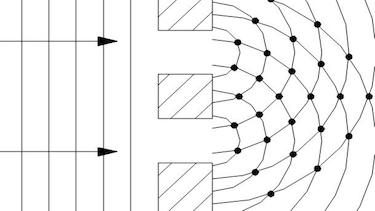
4 Double Slit Interference
double slit interference

A Light wave passes through a double slit. If the width of the slits is smaller than the wavelength of the laser light, the light is diffracted into cylindrical waves. The Huygens-Fresnel principle states that each point can be considered as a secondary wavefront.

The two wavefronts are superimposed. There is destructive and constructive interference, depending wether there is a phase shift between the two wafefronts or not at the meeting point. On a screen one will find bright and dark spots due to this interference.

5 Calculating the wavelength
sketch for calculating the wavelength

Given distance between the two slits a, the distance between slit and screen D and the measured distance between two maximas x, the wavelength of the light source can be determined.
$\sin{\alpha}=\frac{\Delta s}{a}\approx \frac{x}{D}$

Here we use the small angle approximation, which is valid for small angles $\alpha$. If $\Delta s$ is a multiple of the wavelength one can write:

$$\lambda = \frac{a\cdot x}{k\cdot D},~ \text{with}~ k\in \mathbb{N}$$

Note that each number of $k$ stands for the next maxima.

6 interference on thin layers
interference on thin layers

Interference on thin layers offers a wide variety of fabulous colors. If the sun light shines on thin partly reflective layers, to a certain color occurs destructive interference. So if the additional path of the light $2\Delta$ is half a multiple of the wavelength, the color will be taken off.

$$2\Delta=n\cdot \lambda - \frac{\lambda}{2}$$

sources:
M. Kramer, "Physik als Abenteuer", Band 1, Aulis Verlag, 2011
J. Blum, Christian German School Chiang Mai, Thailand, 2017
K. Johnson et. al., "Advanced Physics for you", Oxford, 2015
Wikipedia, "double slit experiment"



Question 1 circular waves

Two circular waves with a distance of 4 cm have a wavelength of 0.5 cm.

  1. Draw the wavefronts of the two waves in order two obtain the interference pattern.
  2. Describe what happens if two wavefronts meet and in between.
  3. Describe what happens if a trough from the one wave meets a crest from the other wave.
  4. Imagine this two waves would be soundwaves and you would walk along a straight line through the interference pattern. Describe what you would har.
  5. Determine the optical path difference Δs which is necessary for destructive interference.

circular water waves


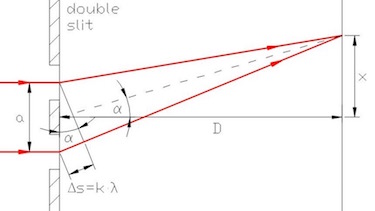
Experiment 1 Double slit experiment

sketch of double slit experiment

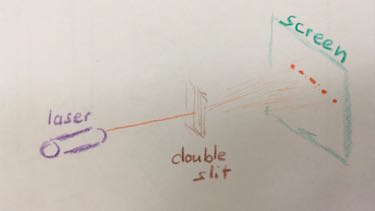
You will need a double slit, laser light and a screen.

  1. Take a photo of your setup.
  2. Note the slit width and the wavelenght of the laser. Measure the distance between slit and screen.
  3. Measure the distance between the first and second and third maximum.
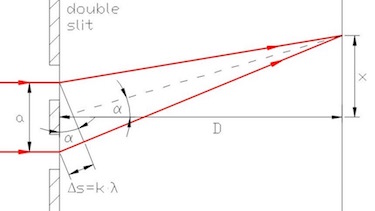
  4. Check the formula: $$\lambda = \frac{a\cdot x}{k\cdot D},~ \text{with}~ k\in \mathbb{N}$$


First relax ...

Did you know that the colors of a hummingbird are a result of thin layer interference?

Question 2 double slit interference

A red laser with a wavelength of 630 nm and a green laser with 530 nm is used.The slit width ist 500 nm, the two slits are sperated 2 mm and the distance between slit and screen is 70 cm

  1. Calculate the position $x$ of the maxima on the screen for the red light.
  2. Calculate the position $x$ of the maxima on the screen for the green light.
  3. Draw the interference pattern on the screen for 3 orders of maxima.
Fisch im Aquarium



Question 3 Refraction with the wave model

refraction of light

A wave with the wavelength of 500 nm is hitting the surface at an angel of 45 °. As medium we use air and glas with a refractive index of 1.45.

  1. Describe the defraction in the wave model.
  2. Draw the wavefront of the incident wave.
  3. Construct the wavefront of the refracted wave.
  4. Measure the refracted angle $\delta_2$.



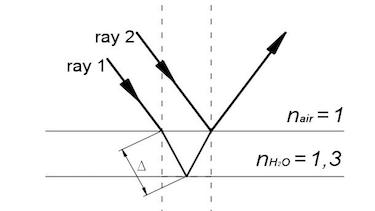
Question 4 Interference on thin layers

The soapbubbles do have faboulos colors.

  1. Name the color which is created if blue, green or red light is wiped out.
  2. Calculate the optical path difference which is nescessary to wipe out these colors.
  3. Calculate the thickness of the soapbubble.
  4. Argue why do the colors of a soapbubble always change and why does the soapbubble burst after a certain time.
soapbubble



Terms and phrases



diffraction the spreading of waves into the area of the geometrical shadow
interference superimposed waves which are amplified or wiped out
constructive and destructive interference Constructive interference occurs if two wavefronts do not have any optical path difference. Destructive interference occurs if the optical path difference is half the wavelength.
single slit interference The diffraction at a single slit causes interference.
double slit interference Interference due to different wavefronts form two slits.
interference on thin layers on thin layers the optical path difference is so small that interference occurs.

© mylime.info